The Problem
Traced-out fibrils are connected to one another, rather than being individual entities.
Ideal Result
Fibrils are long and have relatively small curvature values throughout the entire length of the fibril.
The Process
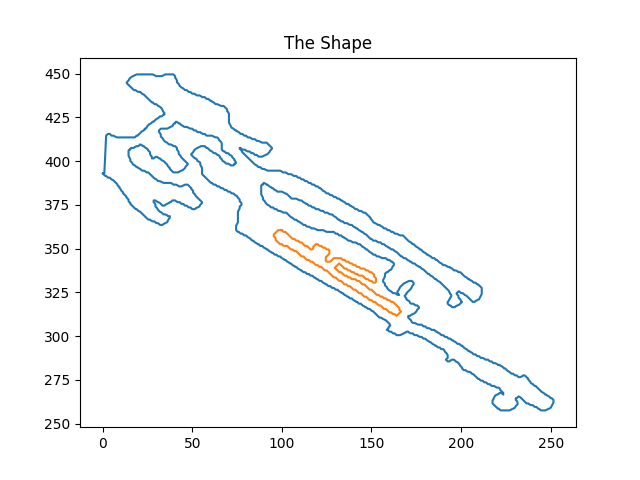
First, we present a selected set of combined fibrils that demonstrate this problem -
Let's try to visualize the curvature at every point. Curvature can be defined for a parameterized curve as
$$ k = \frac{|x'y''-y'x''|}{\left(x'^2-y'^2\right)^{3/2}} $$
For our parameterization, we have points separated by $t=0.5$, and $f(t) = (x(t),y(t))$. After working this calculation out in code, we get
It looks like it worked great! However, there are some points where the "rough terrain" along our curve increase local curvature where it shouldn't be. Let's smooth our data out by using a Savitzky-Golay filter (with win_size=20 & deg=3 polynomial).
Let's isolate these curvature extrema.
At this point, it'd be prudent to visualize what we'd ideally & realistically like this to turn into following curvature estimation.
I say "ideal" - though it isn't, as we see some fibrils cut off early. However, it's important to keep in mind how we go about this process. My thoughts are,
- High-curvature areas should only match with curves across a closed shape (the line drawn between must lie inside the polygon, rather than outside).
- The closest ID'd matching curve must have some minimum arc-length distance away from the initial curve, to avoid matching along the initial curve or those beside it.
- When a shape is matched, get rid of nearby on-line identified curves to prevent oversegmentation.
Note: Notice the blue lines as well - these are unideal consequences of this method. Need to consider how to deal with these. Also, need to add a "minimum area" filter - maybe "if below mean area, don't do curvature segmentation?"
After applying the three criterion, we get this:
As you can see, it needs some work.
First thing: I'm checking for the midpoint between points to see if it lies within the shape. This isn't quite enough - so let's interpolate along the line between curvatures, say, 10 times, and check to see if all of those points lie within instead.
Much better. Second thing, we have connections reaching all the way across the shape. Let's add a max_spatial_distance=20 parameter.
Next, let's add some support for our shape in the middle.
Okay - finally, let's make sure our subdivided polygons aren't too small. We'll take a look at every connection and subdivide the Polygon based on that, using Shapely's split function, then check the area of each with a flat minimum area of min_area=300 pixels for now.
Taking a look at the segmentation,
It looks like the segmentation isn't working properly on interior shapes. Taking a look at the documentation for the split function, we see:
If the splitter does not split the geometry, a collection with a single geometry equal to the input geometry is returned.
Since we're splitting then moving on to the next line, then we're just returning the original shape for both of the lines connecting to the hole.
Doing some work to get the script to recognize our two segments, I first tried to use a convex hull between the two lines, then find the intersection between the hull and the shape itself.
It recognized our shape! Yay! Except ... it looks weird. The convex hull intersection may not really be what we're looking for. Since we have the individual coordinate points of the shapes themselves, let's just construct a shape composed of the two lines and the segments connecting the four verticies. More complicated in setup, but simplier in design.
After wrangling with list comprehension for some time,
Boom. An untested, generalized approach to curvature-based segmentation of polygons! Let's implement this in a class, then return to our timeseries segmentation. We'll likely have to refine our model some in practice, but the broad strokes are there to be worked with.











